This is the first out of a series of posts where I do a Deep Dive (DD) into DL and LLMs and learn as much as I can about how to work with them, fine-tuning, pretraining, vision models, etc. I aspire to do ML research and work on tools for thought and I need to get good in order to do these.

Why go bottom-up?

I found myself becoming too much of a API monkey recently. Constantly searching for tutorials and abstracted platforms to do a lot of the ML work that I wanted to do like

• fine-tuning models for downstream tasks
• using models blindly without understanding what they're ideal for / how they work (MoEs, I'm looking at you)

So in order to really understand the fundamentals, I decided to do the courses (post about this later) and to build something every week but not just anything. It has to be something where

• I have some exposure to the internal workings of the models that I am using (either by building them or some other means)
• The core ML work does not involve a remote API (i.e can't just make an endpoint on HuggingFace)
• it is publicly facing. I should be able to prove that I did this (Loom or Github or some easily verifiable method)

What did I build?

In short, I built a reverse-mode automatic diffrentiation engine in Rust called minigrad. Why reverse-mode ? Because it is harder. And because this is the industry standard. Furthermore its more efficient.

How exactly does autograd work ? This was the question I aspired to answer. I've used it countless times but have never delved into the details. Computing derivatives automatically for such complex models seems magical almost. But I wanted to figure it out.

To briefly explain this process, imagine an equation below

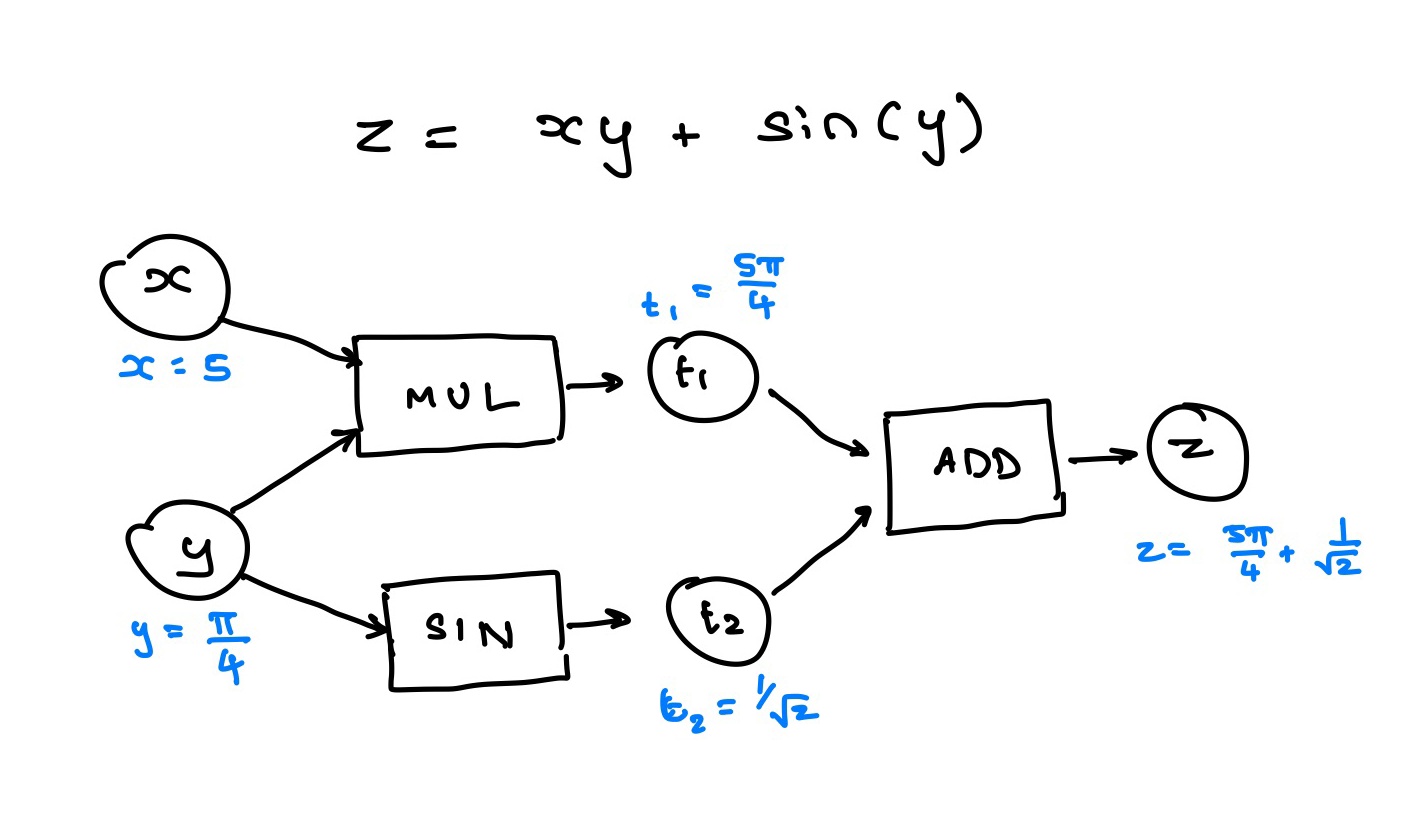
How would you compute the derivative of z w.r.t x and y with this ? Applying the chain rule. You have to build a graph of what operations were applied with what inputs and outputs. Now note that you cannot compute the derivatives during the "forward pass" becuase you need the derivative of the result of the computation w.r.t to the output. So you need to compute the forward pass and then store the intermediate results and then trigger a backward pass, typically with z.backward()

What does this backward graph look like ?

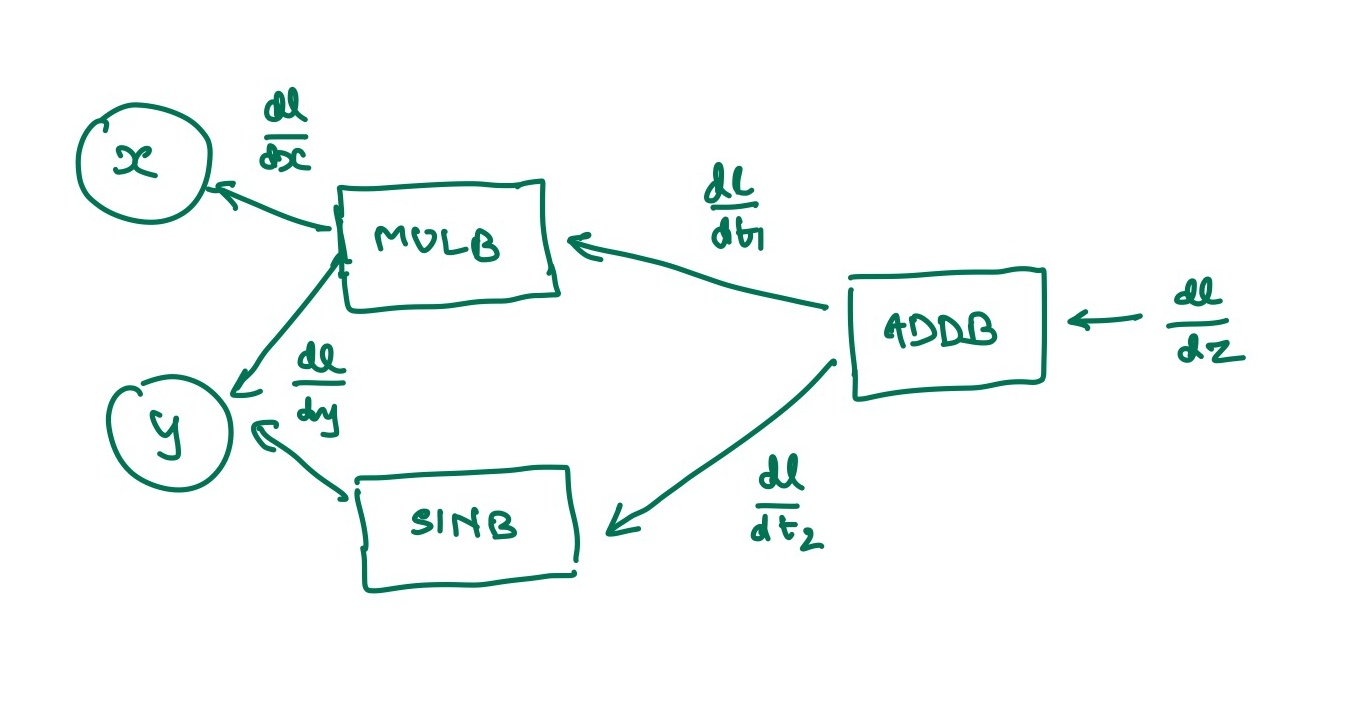
So, how did I build this backward graph in Rust?. I used a tape based mechanism.

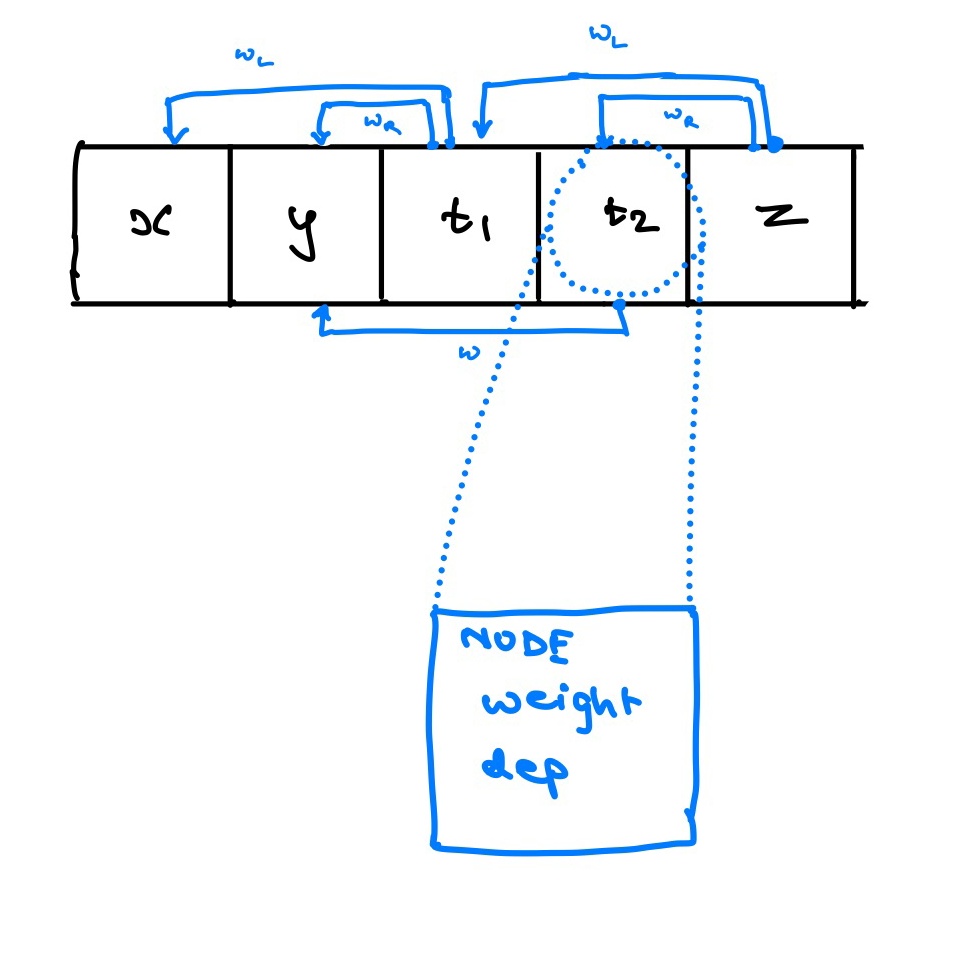
Each of the elements of the tape are Nodes. Each node contains the indices of its dependencies along with the weights of these dependencies. These are calculated on the forward pass. The backward pass the grad function would involve the following

 let mut derivates: Vec<Tensor> = vec![];
initialize_derivates(&mut derivates, &self.tape.unwrap());

// Set the derivative of the current variable wrt itself as 1
derivates[self.index] = derivates[self.index].ones_like().unwrap();

// Go backwards from the outputs to the inputs and calculate the derivatives at each step.
for i in (0..len).rev() {
    let node = &nodes[i];

    // Calculate the derivative using the VJP formula.
    let deriv = derivates[i].clone();

    // if y = xw
    // df/dx = x^t df/fy
    let lhs = node.weight[0].t().unwrap().matmul(&deriv).unwrap();
    println!("The lhs calculated is {}", lhs);
    derivates[node.deps[0]] = (&derivates[node.deps[0]] + lhs.t()).unwrap();

    // df/dw = df/fy w^t
    let rhs = deriv.matmul(&node.weight[1].t().unwrap()).unwrap();
    println!("The rhs calculated is {}", rhs);
    derivates[node.deps[1]] = (&derivates[node.deps[1]] + rhs.t()).unwrap();
}

// Return a gradient object of all the derivates.
Gradient::from(derivates)

This worked to a certain extent. I'll explain that below.

What worked, what didn't

The tape based mechanism worked wonderfully well. I was initially thinking of using a DAG but that would have been a nightmare with Rust's mutable reference rule. This mechanism was suggested by Rufflewind in his excellent blog about automatic diffrentation.

What didn't work were the VJPs - Vector Jacobian Products. These worked well for the multiplication operation because that's naturally a VJP

However for reduction operations and activation functions this was not easy to rectify. Like for a vector of shape (1, n), the sum operation failed to diffrentiate using the same code as above because of size mismatches when multiplying. Recitfying this would involve adopting the stance that Pytorch and TensorFlow use - gradient functions in the backward pass. I would need to do something like this.

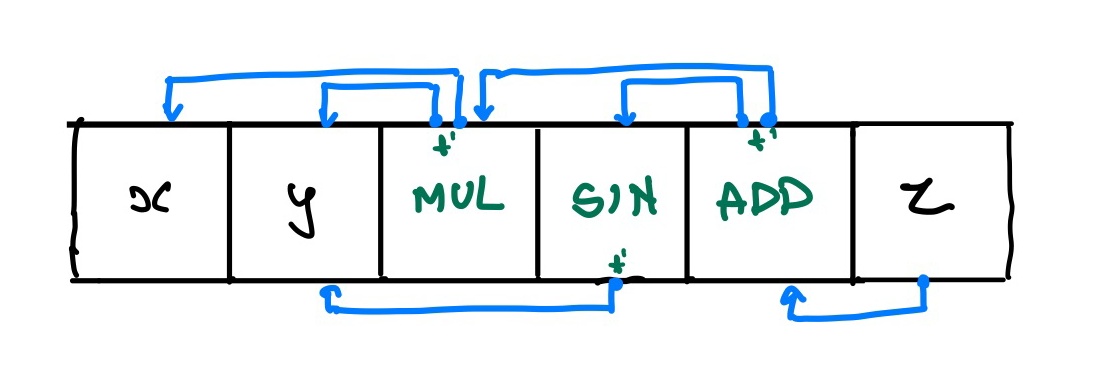
Each of the operations get their own node and have their own backward function when given a backwards propogated gradient. This I believe could solve the problem. However I don't think I have enough time to work on this right now. I'll get to it in a bit when I'm a bit more devious. Now I think I've learned all that I need to for autograd and can confidently move onto the next endeavour.

Lessons Learned

Some of the lessons that I learned while building this are more related to Rust and the meta-problem I'm trying to solve - curiosity

1. Plan when doing it with Rust

One of the cool things about Rust (and one of the daunting things) is the need to think deeply about what you're going to build and how the different pieces interact with each other. A great example is how the Computation Record will be stored to perform the reverse mode. I wanted to do this as a DAG but just by reading about it in Rust, I figured it might be too tedious. That's when I landed on the tape based mechanism. A lot of the other decision I made had to be explicitly stated and thought through. TL;DR Rust is neat.

2. A plan is just a prediction

This might be slightly contradictory to the previous lesson, but I must realize that a plan is just a prediction of the future. Planning is the best when its more than a blueprint but less than the foundation - a scaffold, I think. I kinda got a little stuck with thinking about how to structure everything. Planning is useful and has its place (especially in team settings), but can overplan yourself into a stall (a planning analogue of "tutorial hell"). So the key take away is stay malleable. A plan is just a prediction. Its not a tunnel to see yourself through.

3. Force yourself to ask Why?

This might seem like a banal platitude but often in our world of devices we forget to question why something works as well as it does. Naturally, our current landscape does not promote deep understanding and mastery but we have to take active measures to fight this. Its hard to know what you don't know and harder still to get to know it. But its impossible to know what you don't know you don't know. You have to start somewhere I guess and expand your fractal of actionable knowledge.

Toodles :)